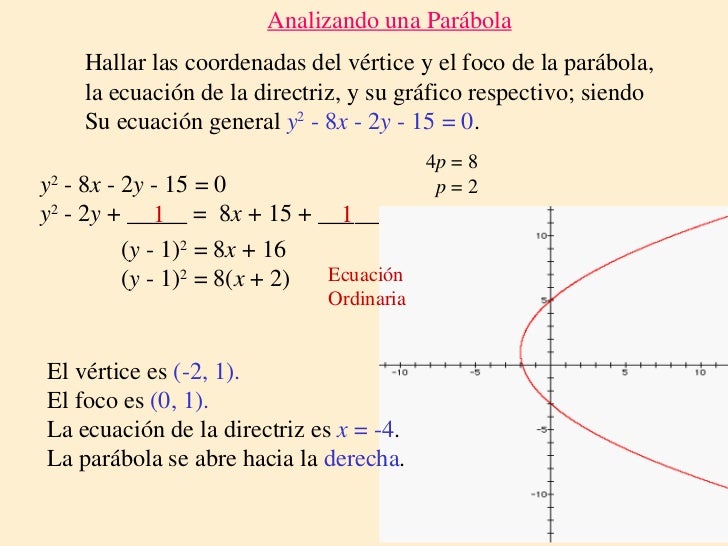
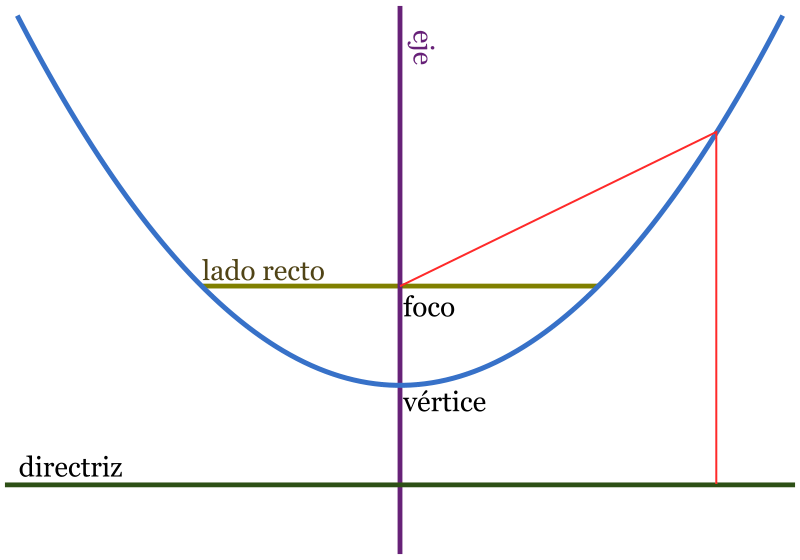
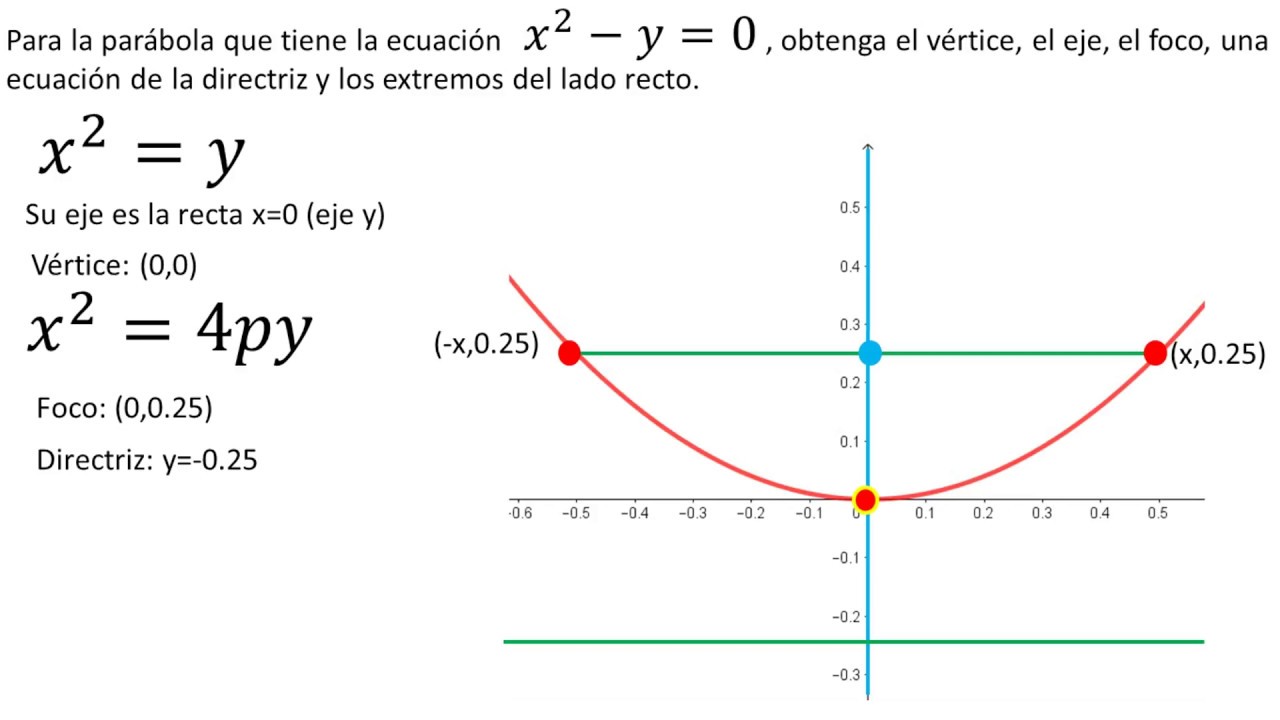
Fórmula general de una parábola. La forma estándar de una ecuación de una parábola con vértice en el origen es y = 4px. Aquí, p representa la distancia entre el vértice y el foco o la directriz. Esta fórmula es fundamental para entender cómo se relacionan el foco, la directriz y el vértice en una parábola.. Una parábola es definida de la siguiente manera: Para un punto fijo, llamado el foco, y una línea recta, llamada la directriz, una parábola es el conjunto de puntos de modo que la distancia hasta el foco y hasta la directriz es la misma. La ecuación de una parábola orientada verticalmente es { { (x-h)}^2}=4p (y-k) (x− h)2 = 4p(y − k).

Ecuación de una parábola Foco, directriz, eje y lado recto YouTube

Ecuación de la parábola dado el vértice y el foco 1 YouTube

Parábola Definición, elementos y propiedades más importantes

Quais são os elementos da parábola? (Peças)

Ecuacion de una parabola si conoces el vertice y el foco YouTube

La ParáBola

GEOMETRÍA ANALÍTICA ECA PARÁBOLA

ELEMENTOS DE UNA PARÁBOLA Curso para la UNAM

Elementos de una parábola Ejemplo 3 YouTube

La parabola

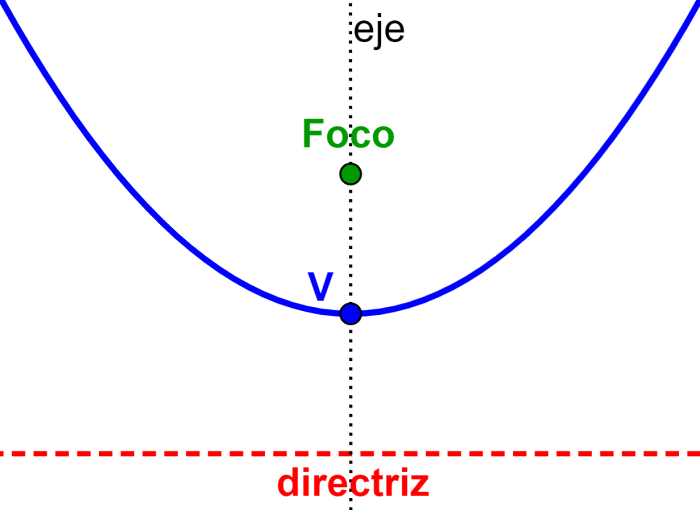
Foco y Directriz de una Parábola Neurochispas

Gráfica y ecuación de la Parábola conociendo foco y directriz YouTube

Elementos de una parábola Ejemplo 1 YouTube

La Parábola y sus Elementos (Vertice, foco, parametro, directriz) YouTube

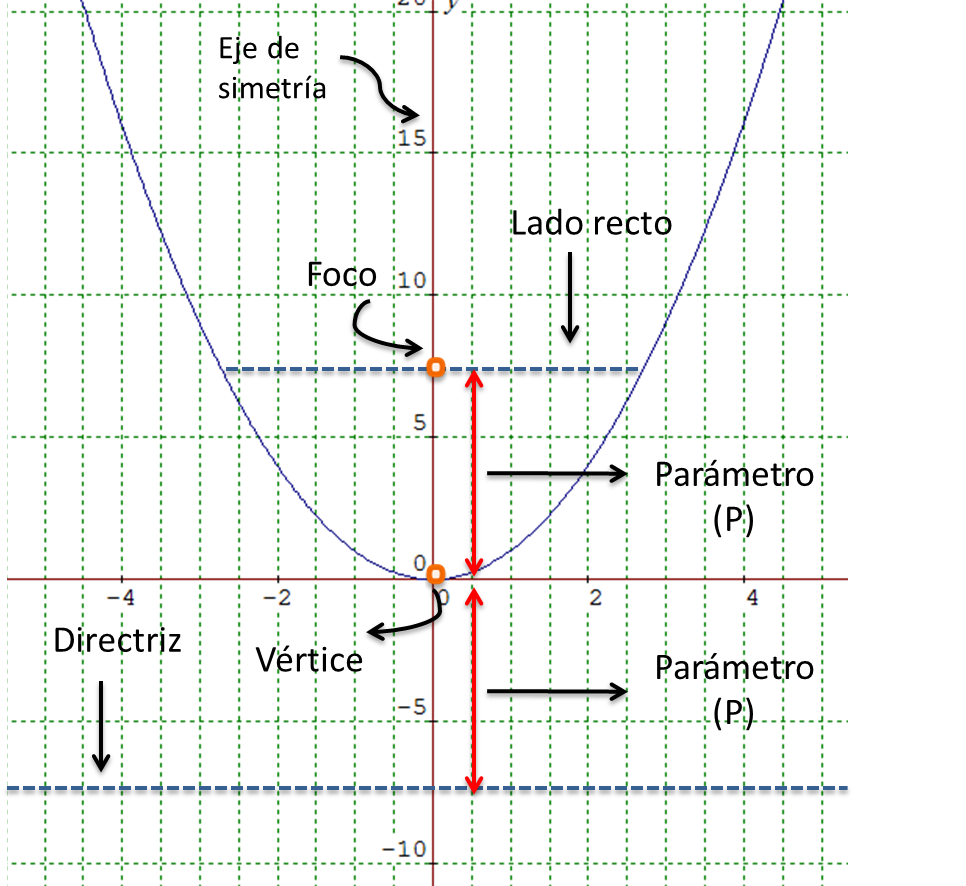
Ecuación de la parábola

Geometria analitica La Parabola

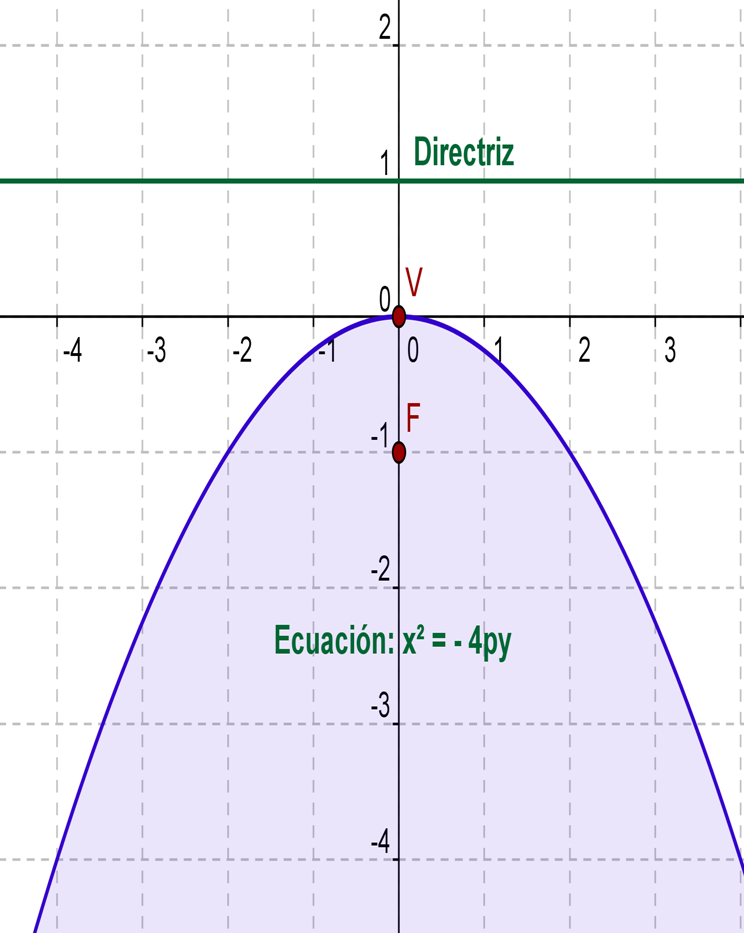
Matemática Paso a Paso La Parábola

Qué es una Parábola Definición de Parábola

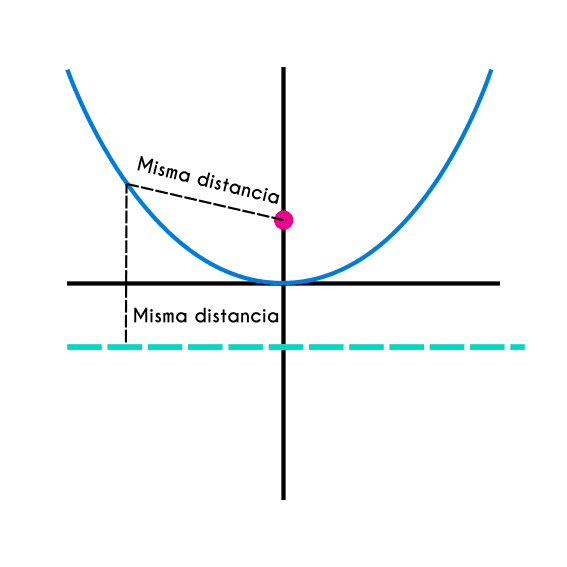
TODAS las Partes de una Parábola Fhybea

Ecuación de la parábola dado el foco y la directriz YouTube

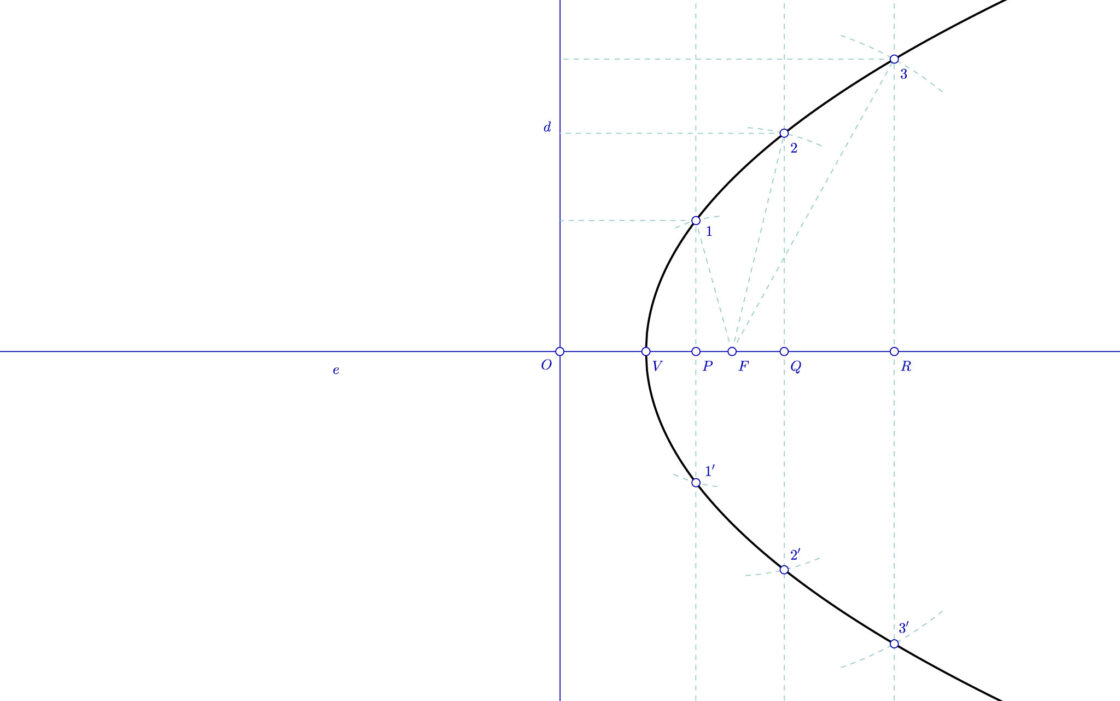
Ecuación de una parábola a partr del foco y la directriz. Dado el foco y la directriz de una parábola, podemos encontrar la ecuación de la parábola. Consideremos, por ejemplo, la parábola cuyo foco está en ( − 2, 5) y la directriz es y = 3 . Empezamos por considerar un punto general ( x, y) en la parábola. Mediante la fórmula de la.. La directriz es una línea horizontal que se encuentra a una distancia fija del foco. Para determinar la ecuación de la directriz de una parábola, necesitamos conocer la forma general de la ecuación de una parábola, que es de la forma y = ax^2 + bx + c. En esta ecuación, a, b y c son constantes que determinan la forma, posición y.