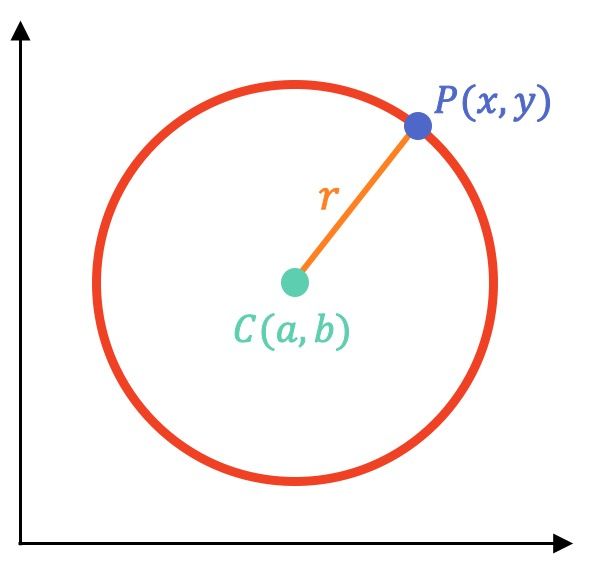
Preparación para secciones cónicas. Practicar determinar mediciones en un círculo, mediante el teorema de Pitágóras y completar el cuadrado, nos ayudará a prepararnos para razonar sobre secciones cónicas (tales como círculos y parabolas). Repasemos algunos conceptos que serán útiles a medida que inicies la unidad de secciones cónicas.. Para comprender las cónicas en su totalidad, es esencial familiarizarse con los elementos fundamentales que las caracterizan. Estos elementos incluyen el foco, la directriz, la excentricidad, el eje mayor, el eje menor, entre otros. Cada uno de estos elementos desempeña un papel crucial en la definición y la comprensión de las cónicas.

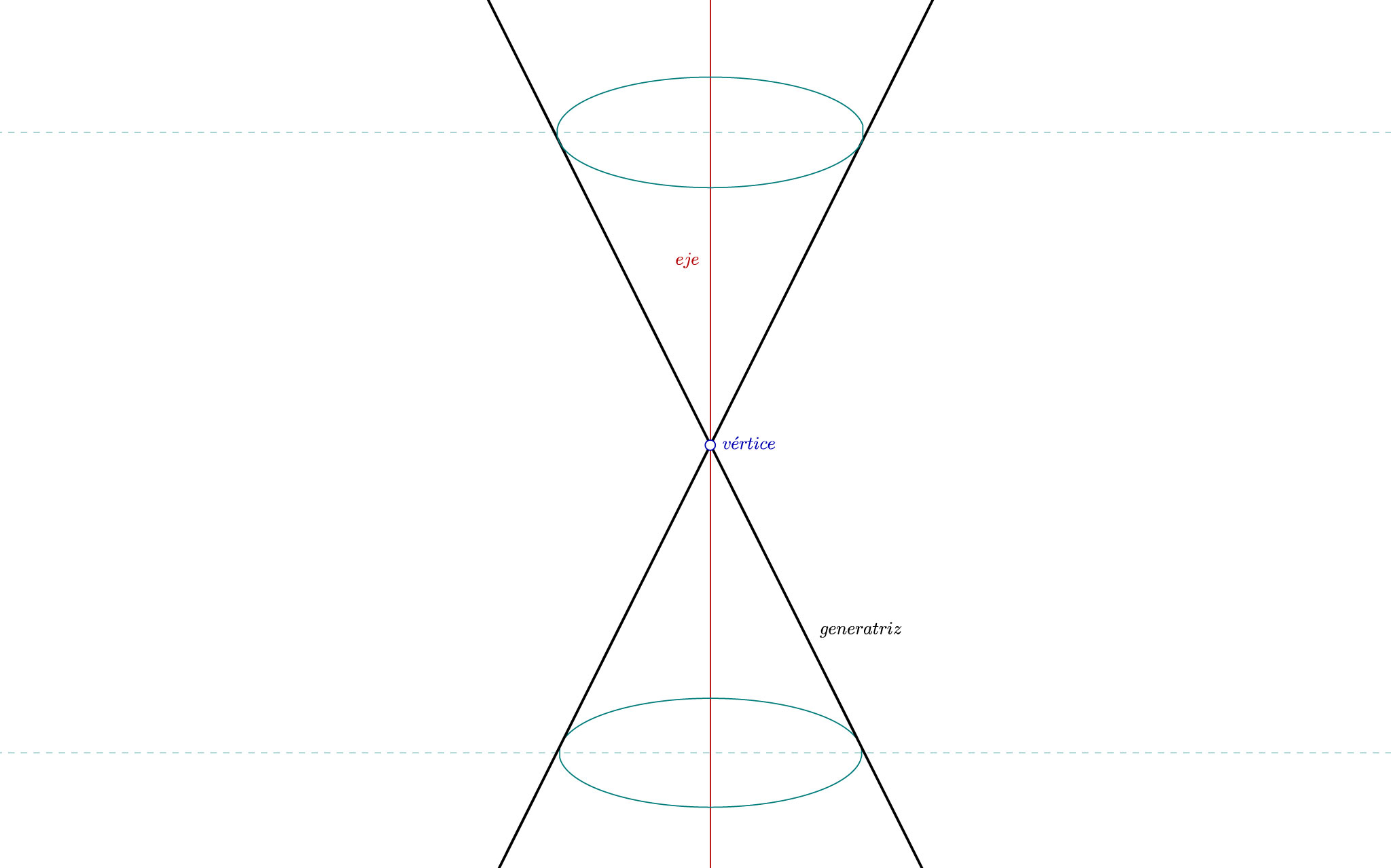
Ejercicios resueltos de cónicas. Superficie cónica de revolución. Eje, generatriz y vértice de

Cónicas

LAS CONICAS Mind Map

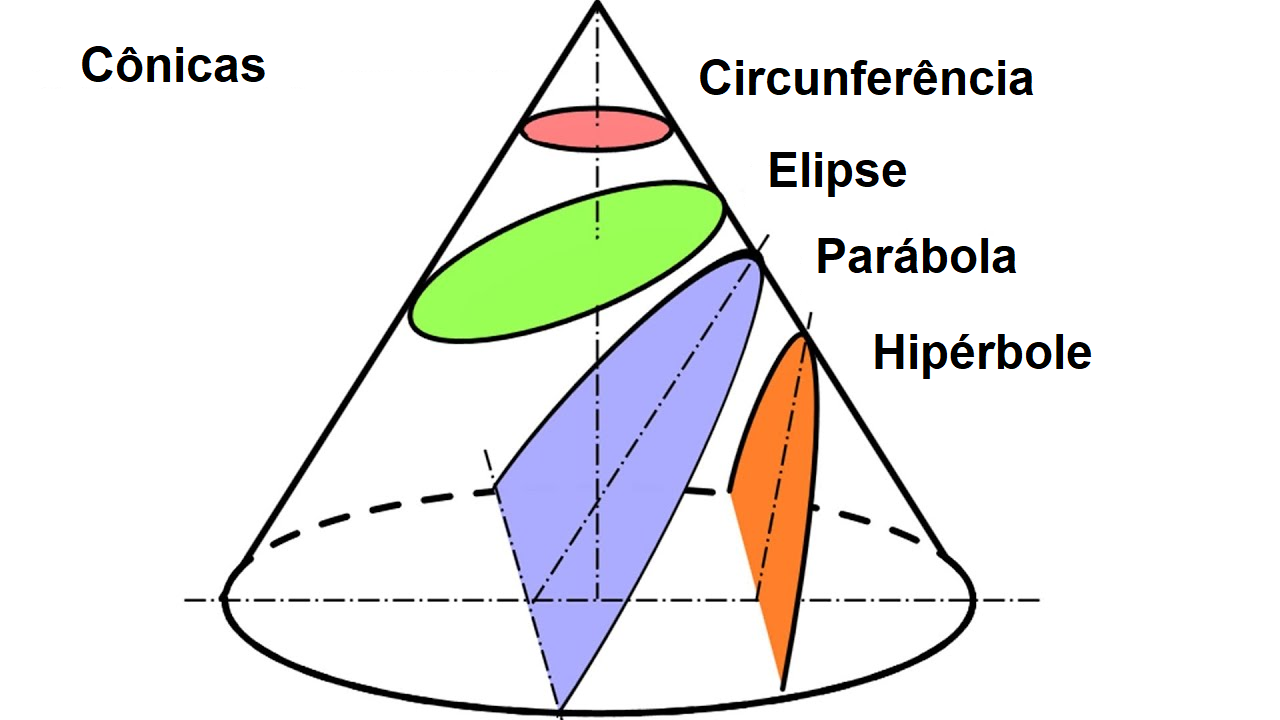
Cônicas NOIC

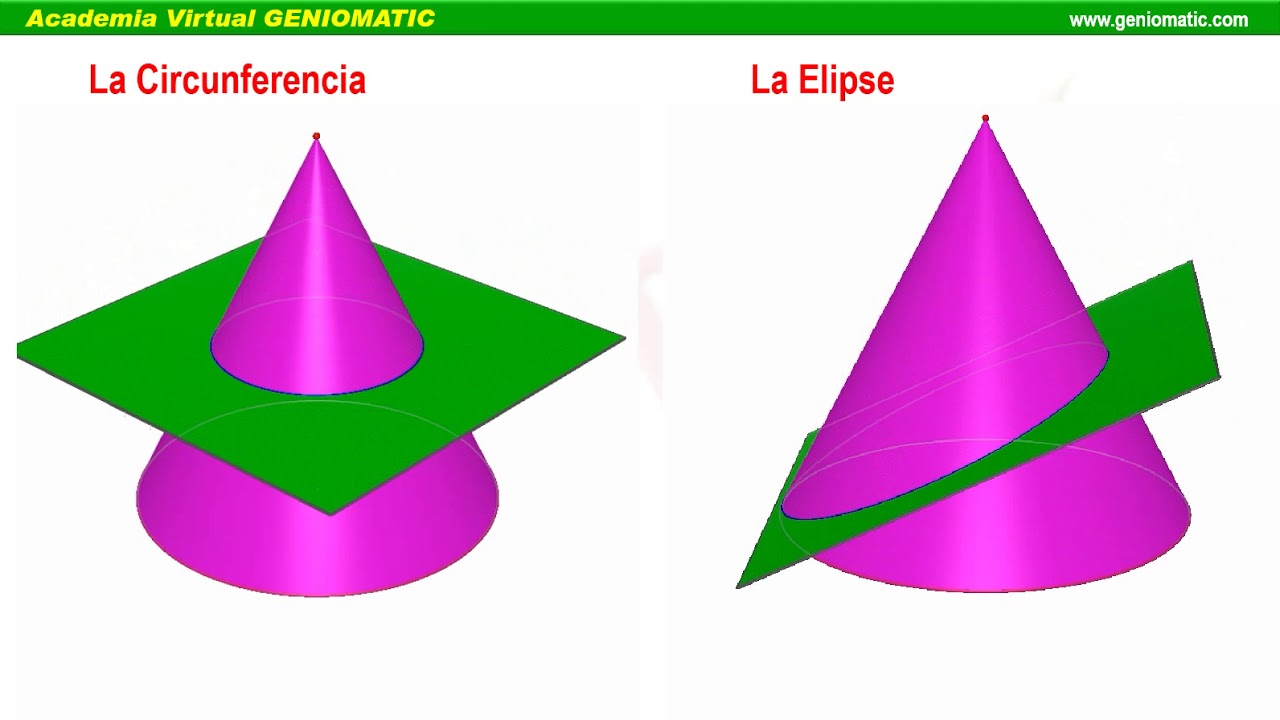
Cónicas Geometría YouTube

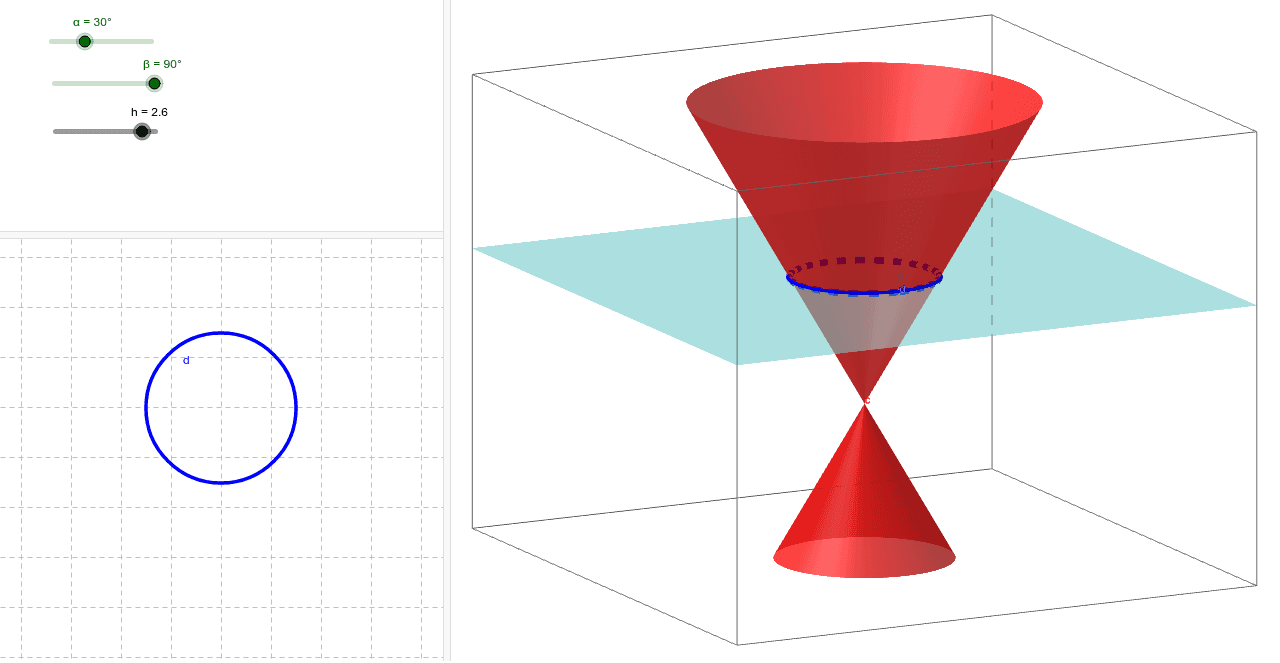
Secciones cónicas GeoGebra

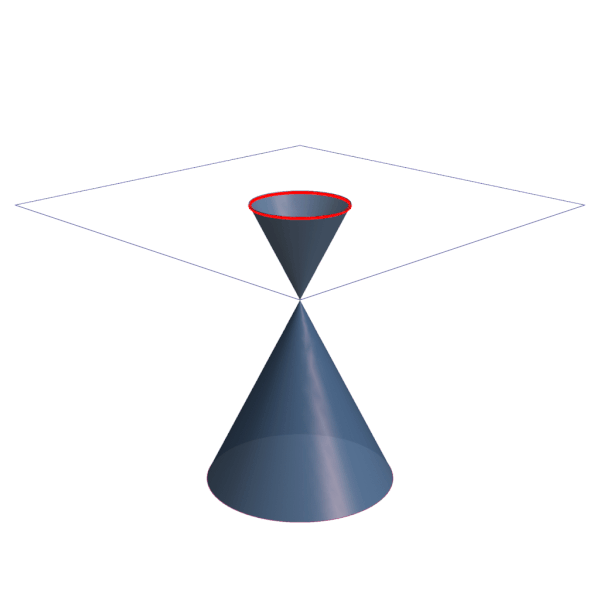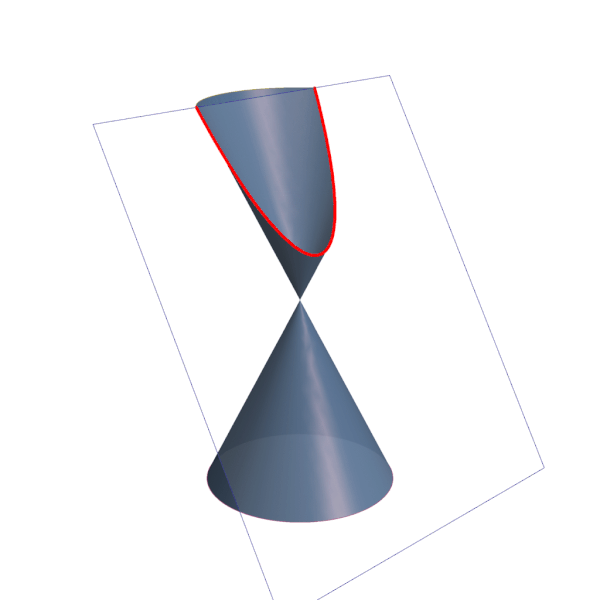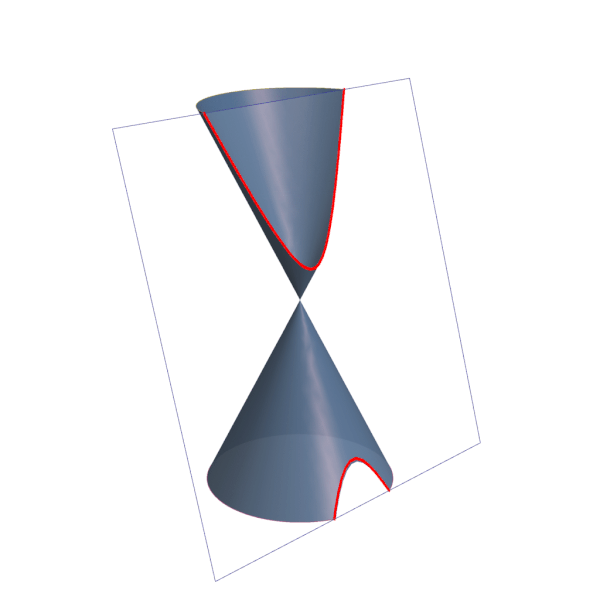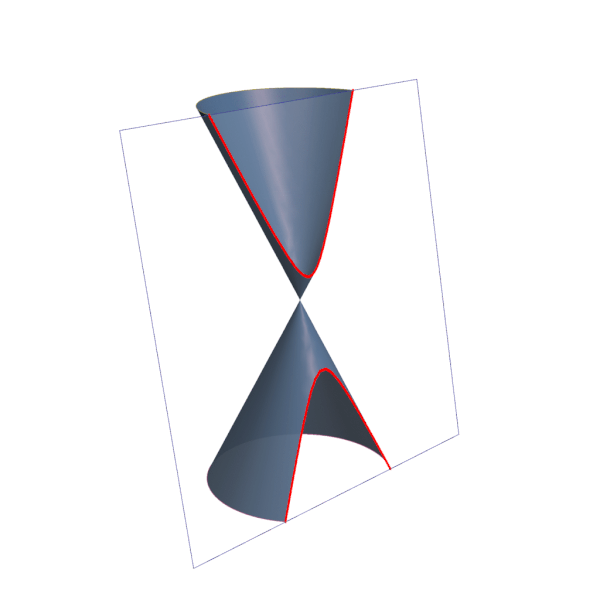
Cônicas Elipse, hipérbole e parábola Toda Matéria

14DIBUJO TÉCNICO CURVAS CÓNICAS, LA ELIPSE INTRODUCCIÓN YouTube

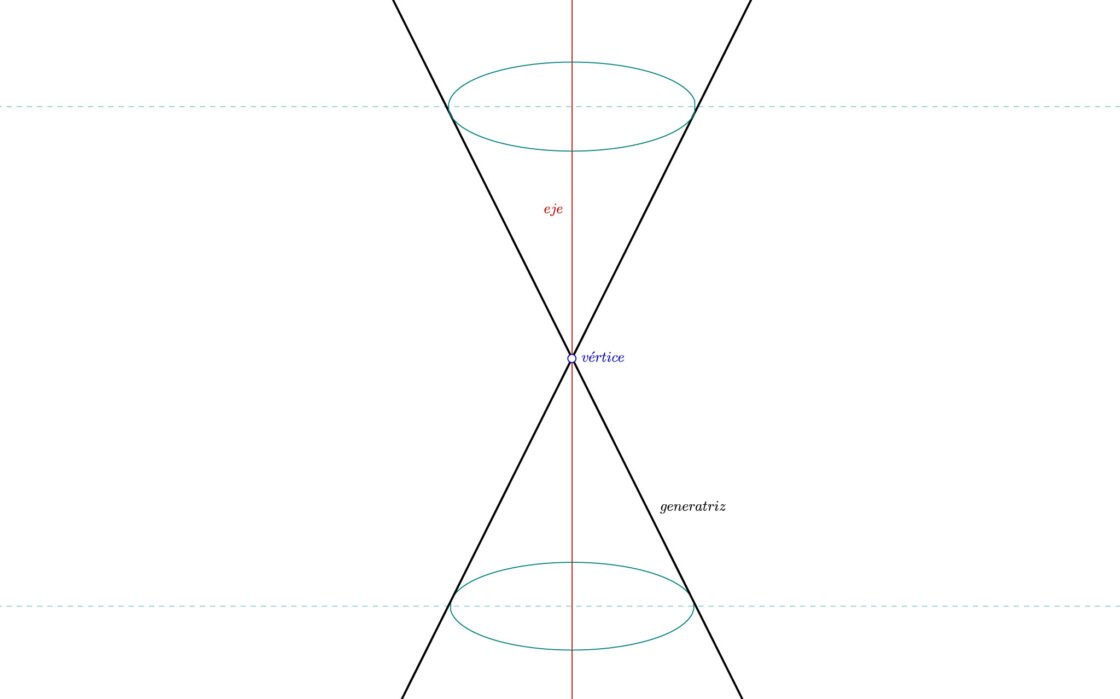
Curvas cónicas Propiedades, clasificación y desarrollo

Secciones cónicas Mi Profe

PPT Geometría Analítica. “ Cónicas ” PowerPoint Presentation, free download ID4615098

Aprendiendo matematica con Dibujo "A" SECCIONES CONICAS

¿Qué son las Secciones Cónicas? (definición, tipos y ejemplos)

5. Secciones Cónicas. Obtener la Ecuación de la cónica a partir de su forma cuadrática. YouTube

Las cónicas La Guía de Matemática

Curvas cónicas Propiedades, clasificación y desarrollo

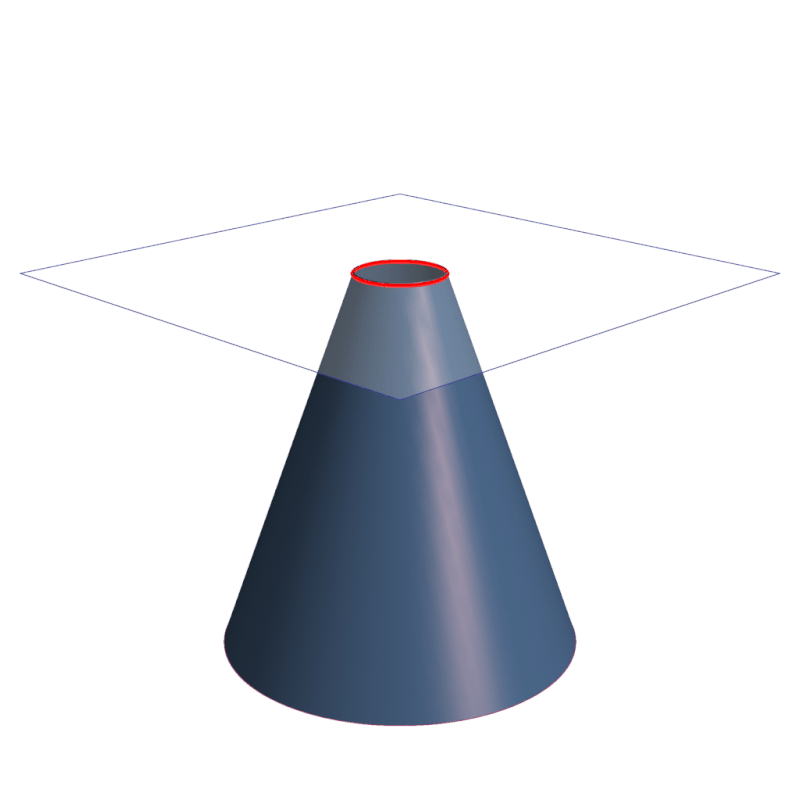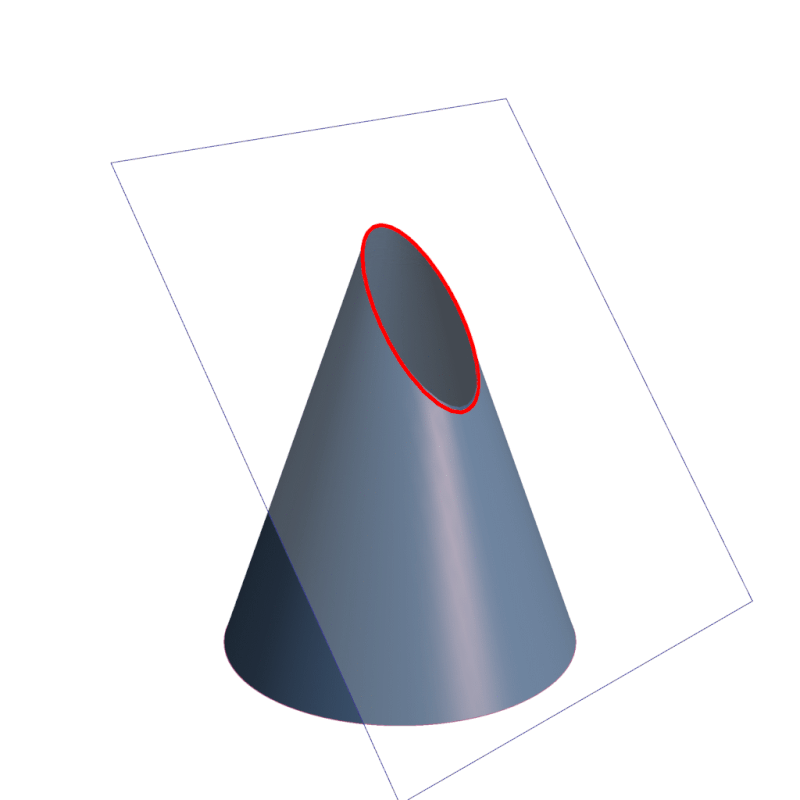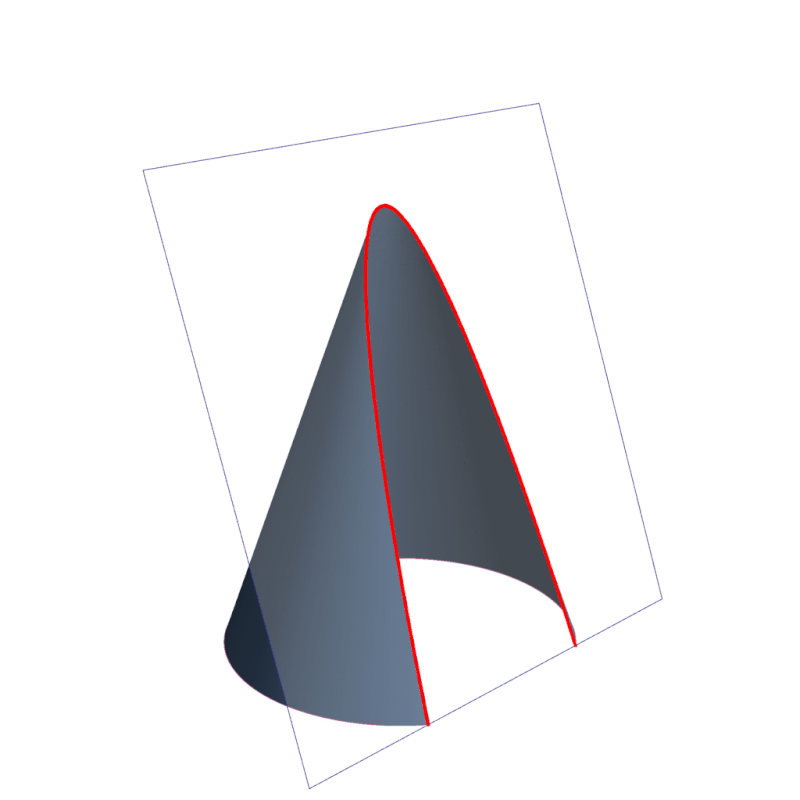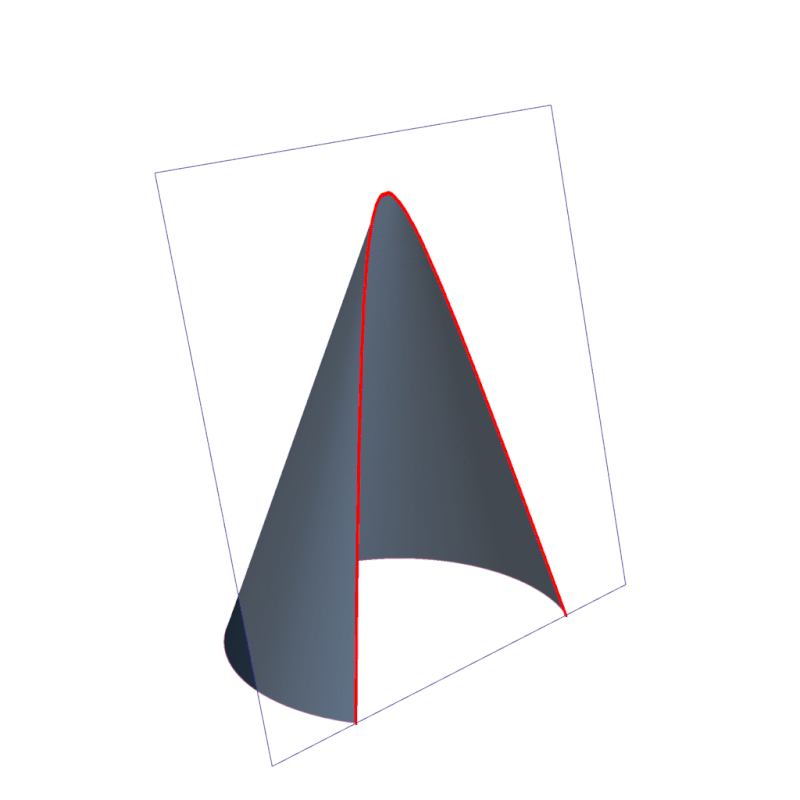
Secciones cónicas tipos, aplicaciones, ejemplos

Cónicas Por mas matemática

Matemática Secciones cónicas

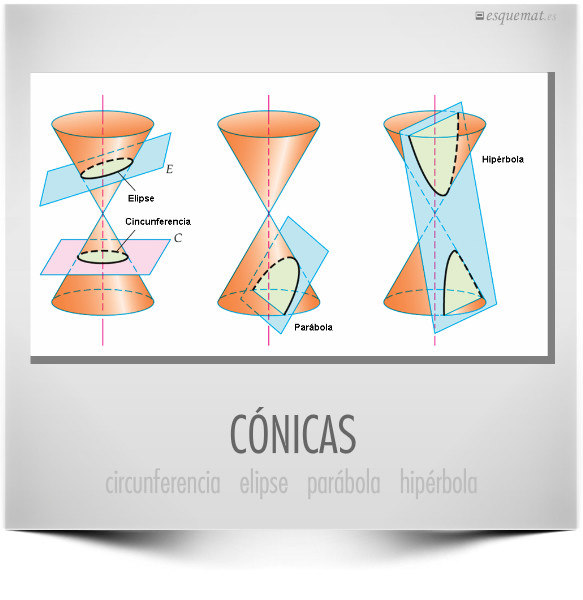
Cónicas Esquemat

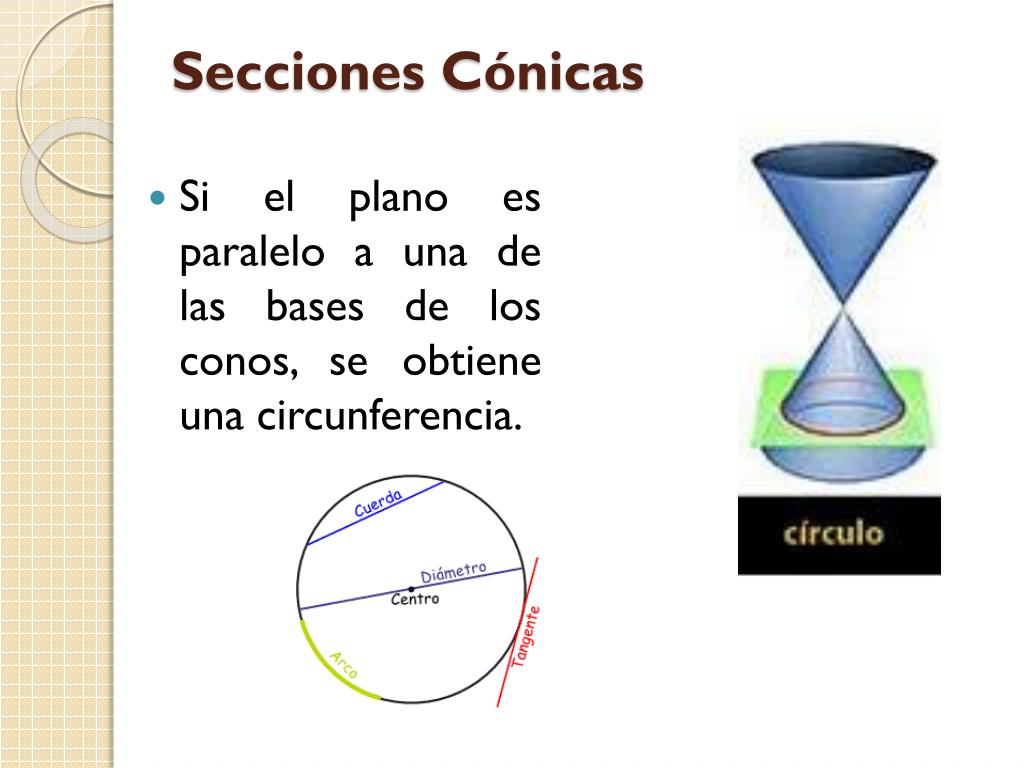
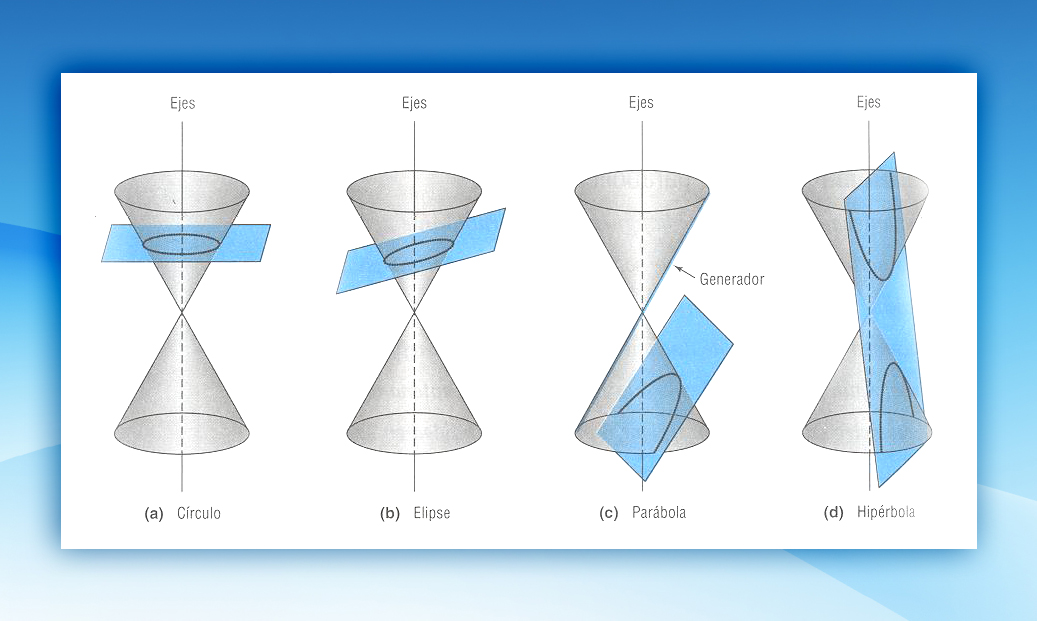
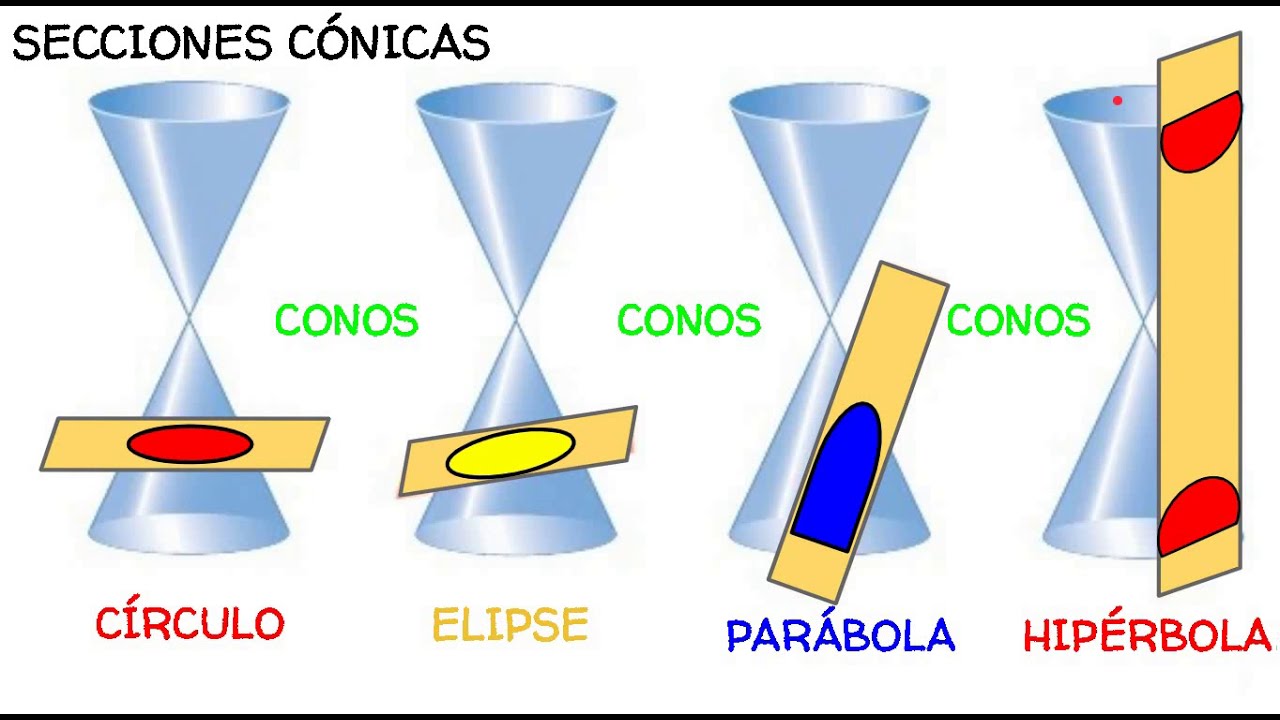
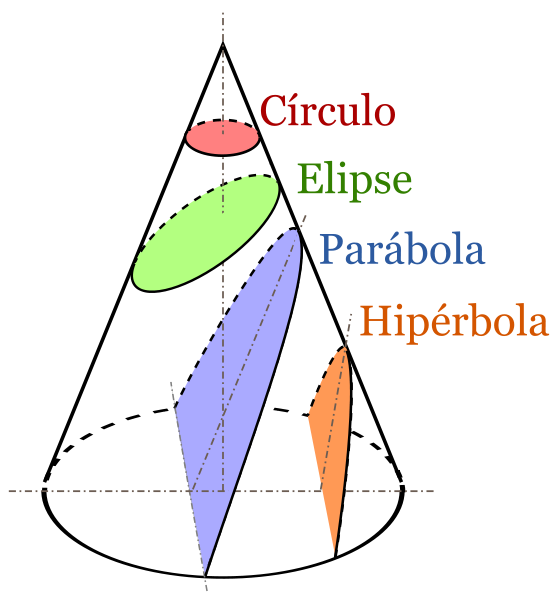
Sección cónica. En matemática, y concretamente en geometría, se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; 1 si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas elipse, parábola, hipérbola y circunferencia .. Las secciones cónicas son las curvas que se obtienen al interceptar un plano con un cono. Hay varias formas de hacer esto; por ejemplo, si el plano se hace pasar perpendicularmente al eje axial del cono se obtiene una circunferencia. Inclinando un poco el plano respecto al eje axial del cono se obtiene una elipse, una curva que es cerrada.